На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних - правого и левого, которые совсем не страшны, несмотря на то что записываются как и .
Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.
Графически функция непрерывна в точке ,
если её график не "разрывается" в этой точке. График такой непрерывной
функции - ![]() показан на рисунке ниже.
показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:
1. Функция определена в точке .
Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 - на рисунке ниже.

Пример 1. Функция f (x ) определена следующим образом:
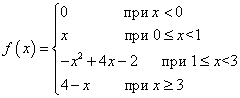
Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0 , x = 1 , x = 3 ?
Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.
Точка x = 0 . Найдём левосторонний предел в этой точке:
![]() .
.
Найдём правосторонний предел:
x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0 .
Точка x = 1 . Найдём левосторонний предел в этой точке:
Найдём правосторонний предел:
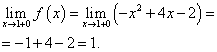
Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
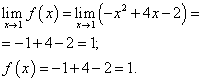 .
.
Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1 .
Точка x = 3 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:
 .
.
Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3 .
Основной вывод: данная функция является непрерывной в каждой граничной точке.
Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение
Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .
Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m , то есть l = f (m ) , m ≥0 .
Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l . Однако если масса груза близка к пределу прочности нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию от точки подвеса до поверхности стола. График функции l = f (m ) изображён на рисунке. На участке этот график является непрерывной (сплошной) линией, а в точке он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках, кроме , функция l = f (m ) непрерывна, а в точке она имеет разрыв.
Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика .
Непрерывность функции на промежутке
Пусть функция y = f (x ) определена в интервале ]a , b [ и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в интервале ]a , b [ . Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b [ , ]a , + ∞[ , ]- ∞, + ∞[ . Пусть теперь функция y = f (x ) определена на отрезке [a , b ] . Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a , оставаясь на отрезке [a , b ] , мы можем приближаться только справа, а к точке b - только слева. Функция называется непрерывной на отрезке [a , b ] , если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b .
Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a , b ] , функция непрерывна на отрезке [0 , b ] , функция непрерывна на любом отрезке, не содержащем точку a = 2 .
Пример 4. Исследовать функцию на непрерывность.
Решение. Проверяем первое условие. Функция не определена в точках - 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах
.Пример 5.
Определить, при каком значении
параметра a
непрерывна на всей области определения
функция

Решение.
Найдём правосторонний предел при :
![]() .
.
Очевидно, что значение в точке x = 2 должно быть равно ax :
![]()
a = 1,5 .
Пример 6.
Определить, при каких значениях
параметров a
и b
непрерывна на всей области определения
функция

Решение.
Найдём левосторонний предел функции в точке :
![]() .
.
Следовательно, значение в точке должно быть равно 1:
Найдём левосторонний функции в точке :
Очевидно, что значение функции в точке должно быть равно :
Ответ: функция непрерывна на всей области определения при a = 1; b = -3 .
Основные свойства непрерывных функций
К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t , выраженная законом s = f (t ) , даёт пример непрерывной функции f (t ) . Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f (t ) .
В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.
1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.
2. Функция f (x ) , непрерывная на интервале [a , b ] , принимает все промежуточные значения между значениями в концевых точках, то есть, между f (a ) и f (b ) . В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.
Рассмотрим две функции, графики которых изображены на рис. 1 и 2. График первой функции можно нарисовать, не отрывая карандаша от бумаги. Эту функцию можно назвать непрерывной. График другой функции так нарисовать нельзя. Он состоит из двух непрерывных кусков, а в точке имеет разрыв, и функцию мы назовем разрывной.


Такое наглядное определение непрерывности никак не может устроить математику, поскольку содержит совершенно нематематические понятия «карандаш» и «бумага». Точное математическое определение непрерывности дается на основе понятия предела и состоит в следующем.
Пусть функция определена на отрезке и - некоторая точка этого отрезка. Функция называется непрерывной в точке , если при стремлении к ( рассматривается только из отрезка ) значения функции стремятся к , т.е. если
![]() . (1)
. (1)
Функция называется непрерывной на отрезке, если она непрерывна в каждой его точке.
Если в точке равенство (1) не выполняется, функция называется разрывной в точке .
Как видим, математически свойство непрерывности функции на отрезке определяется через местное (локальное) свойство непрерывности в точке.
Величина называется приращением аргумента, разность значений функции называется приращением функции и обозначается . Очевидно, что при стремлении к приращение аргумента стремится к нулю: .
Перепишем равенство (1) в равносильном виде
![]() .
.
Используя введенные обозначения, его можно переписать так:
Итак, если функция непрерывна, то при стремлении приращения аргумента к нулю приращение функции стремится к нулю. Говорят и иначе: малому приращению аргумента соответствует малое приращение функции. На рис. 3 приведен график непрерывной в точке функции, приращению соответствует приращение функции . На рис. 4 приращению соответствует такое приращение функции , которое, как бы мало ни было, не будет меньше половины длины отрезка ; функция разрывна в точке .


Наше представление о непрерывной функции как о функции, график которой можно нарисовать, не отрывая карандаша от бумаги, прекрасно подтверждается свойствами непрерывных функций, которые доказываются в математическом анализе. Отметим, например, такие их свойства.
1. Если непрерывная на отрезке функция принимает на концах отрезка значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю.
2. Функция , непрерывная на отрезке , принимает все промежуточные значения между значениями в концевых точках, т.е. между и .
3. Если функция непрерывна на отрезке, то на этом отрезке она достигает своего наибольшего и своего наименьшего значения, т.е. если - наименьшее, а - наибольшее значения функции на отрезке , то найдутся на этом отрезке такие точки и , что и .
Геометрический смысл первого из этих утверждений совершенно ясен: если непрерывная кривая переходит с одной стороны оси на другую, то она пересекает эту ось (рис. 5). Разрывная функция этим свойством не обладает, что подтверждается графиком функции на рис. 2, а также свойствами 2 и 3. На рис. 2 функция не принимает значения , хотя оно заключено между и . На рис. 6 приведен пример разрывной функции (дробная часть числа ), которая не достигает своего наибольшего значения..
Сложение, вычитание, умножение непрерывных на одном и том же отрезке функций вновь приводят к непрерывным функциям. При делении двух непрерывных функций получится непрерывная функция, если знаменатель всюду отличен от нуля.
К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время непрерывны, и зависимость, например, пути от времени , выраженная законом , дает пример непрерывной функции .
С помощью непрерывных функций описывают состояния и процессы в твердых телах, жидкостях и газах. Изучающие их науки - теория упругости, гидродинамика и аэродинамика - объединяются одним названием - «механика сплошной среды».
Непрерывные функции образуют основной класс функций, с которыми оперирует математический анализ. Представление о непрерывной функции можно получить, если сказать, что график ее непрерывен, т.е. его можно начертить, не отрывая карандаша от бумаги.
Непрерывная функция математически выражает одно свойство, с которым нам приходится часто встречаться на практике, заключающееся в том, что малому приращению независимой переменной соответствует малое же приращение зависимой от нее переменной (функции). Прекрасными примерами непрерывной функции могут служить различные законы движения тел \(s=f(t)\) , выражающие зависимости пути \(s\) , пройденного телом, от времени \(t\) . Время и пространство непрерывны, при этом тот или иной закон движения тела \(s=f(t)\) устанавливает между ними определенную непрерывную связь, характеризующуюся тем, что малому приращению времени соответствует малое же приращение пути.
К абстракции непрерывности человек пришел, наблюдая окружающие его, так называемые сплошные среды - твердые, жидкие или газообразные, например металлы, воду, воздух. На самом деле, как теперь хорошо известно, всякая физическая среда представляет собой скопление большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходится иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды без всяких просветов, непрерывно распределенной в занятом ею пространстве. На таком допущении базируются многие физические дисциплины, например гидродинамика, аэродинамика, теория упругости. Математическое понятие непрерывности играет, естественно, в этих дисциплинах, как и во многих других, большую роль.
Рассмотрим какую-либо функцию \(y=f(x)\) и вполне определенное значение независимой переменной \(x_0\) . Если наша функция отражает некоторый непрерывный процесс, то значениям \(x\) , мало отличающимся от \(x_0\) должны соответствовать значения функции \(f(x)\) мало отличающиеся от значения \(f(x_0)\) в точке \(x_0\) . Таким образом, если приращение \(x-x_0\) независимой переменной мало, то должно быть малым также и соответствующее приращение \(f(x)-f(x_0)\) функции. Иными словами, если приращение независимой переменной \(x-x_0\) стремится к нулю, то приращение \(f(x)-f(x_0)\) функции должно, в свою очередь, стремиться к нулю, что может быть записано следующим образом:
\(\lim_{x-x_0\to0}\Bigl=0.\)
Это соотношение и является математическим определением непрерывности функции в точке \(x_0\) .
Функция \(f(x)\) называется непрерывной в точке \(x_0\) , если выполняется равенство (1).
Дадим еще такое определение:
Функция называется непрерывной для всех значений, принадлежащих к данному отрезку, если она непрерывна в каждой точке \(x_0\) этого отрезка, т.е. в каждой такой точке выполняется равенство (1).
Таким образом, для того чтобы ввести математическое определение свойства функции, заключающегося в том, что график ее есть непрерывная (в обычном понимании этого термина) кривая, появилась необходимость определить сначала локальное, местное свойство непрерывности (непрерывность в точке \(x_0\) ), а затем на этой основе определить непрерывность функции на целом отрезке.
Приведенное определение, впервые указанное в начале прошлого столетия Коши, является общепринятым в современном математическом анализе. Проверка на многочисленных конкретных примерах показала, что это определение хорошо соответствует сложившемуся у нас практическому представлению о непрерывной функции, например представлению о непрерывном графике.
В качестве примеров непрерывных функций могут служить известные из школьной математики элементарные функции \(x^n,\) \(\sin{x},\) \(\cos{x},\) \(a^x,\) \(\lg{x},\) \(\arcsin{x},\) \(\arccos{x}\) . Все перечисленные функции непрерывны на отрезках изменения \(x\) , где они определены.
Если непрерывные функции складывать, вычитать, умножать и делить (при знаменателе, не равном нулю), то в результате мы снова придем к непрерывной функции. Однако при делении непрерывность, как правило, нарушается для тех значений \(x_0\) , при которых функция, стоящая в знаменателе, обращается в нуль. Результат деления представляет собой тогда разрывную в точке \(x_0\) функцию.
Функция \(y=\frac{1}{x}\) может служить примером разрывной в точке \(y=0\) функции. Ряд других примеров разрывных функций дают графики, изображенные на рис. 1.
Рекомендуем внимательно рассмотреть эти графики. Отметим, что разрывы функций бывают разные: иногда с приближением \(x\) к точке \(x_0\) , где функция претерпевает разрыв, предел \(f(x)\) существует, но отличен от \(f(x_0)\) , а иногда, как на рис. 1в, этого предела просто не существует. Бывает и так, что с приближением \(x\) к \(x_0\) с одной стороны \(f(x)-f(x_0)\to0\) , а если \(x\to x_0\) , приближаясь с другой стороны, то \(f(x)-f(x_0)\) уже не стремится к нулю. В этом случае, конечно, мы имеем разрыв функции, хотя про нее можно сказать, что она в этой точке «непрерывна с одной стороны». Все эти случаи можно проследить на приведенных графиках.
Определение непрерывности функции
1. Функция \(y=f(x)\) непрерывна в точке \(x=a\) , если пределы слева и справа равны и равны значению функции в этой точке, т. е.
\(\lim_{x\to a-0}f(x)=\lim_{x\to a+0}f(x)=f(a).\)
2. Функция \(y=f(x)\) непрерывна в точке \(x=a\) , если она определена в этой точке и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. \(\lim_{\Delta x\to 0}\Delta y=0\) вблизи точки \(a\) .
Сумма, разность и произведение конечного числа непрерывных функций есть функция непрерывная.
Непрерывная на отрезке \(\) функция принимает любое промежуточное значение между ее наименьшим \(m\) и наибольшим \(M\) значением, то есть \(m\leqslant f(x)\leqslant M\) для всех \(x\in\) . Отсюда следует, что если в граничных точках отрезка \(\) функция имеет разные знаки, то внутри отрезка есть по крайней мере одно такое значение \(x=c\) , при котором функция обращается в ноль. Это свойство непрерывности функций позволяет находить приближенно корни многочленов.
Точки разрыва функции
Значения аргумента, которые не удовлетворяют условиям непрерывности, называются точками разрыва функции . При этом различают два рода точек разрыва функции.
Если при \(x\to a\) слева функция имеет конечный предел \(k_1\) , а при \(x\to a\) справа функция имеет конечный предел \(k_2\) и \(k_1\ne k_2\) , то говорят, что функция при \(x=a\) имеет разрыв первого рода . Разность \(|k_1-k_2|\) определяет скачок функции в точке \(x=a\) . Значение функции при \(x=a\) при этом может быть равно какому угодно числу \(k_3\) .
Если значение функции при \(x=a\) равно \(k_1\) , то говорят, что функция непрерывна слева; если же \(k_2\) , то говорят, что функция непрерывна справа.
Если \(k_1=k_2\ne k_3\) говорят, что функция имеет в точке \(a\) устранимый разрыв .
Если при \(x\to a\) справа или слева, предел функции не существует или равен бесконечности, то есть \(\lim_{x\to a}f(x)=\infty\) , то говорят, что при \(x=a\) функция имеет разрыв второго рода .
Пример 1. Найти множество значений \(x\) , при которых функция \(y=x^3-2x\) непрерывна.
Решение. Найдем приращение функции
\(\Delta y=(x+\Delta x)^3-2(x+\Delta x)-(x^3-2x)=\Delta x\,(\Delta x^2+3x\Delta x+3x^2-2).\)
При любых значениях переменной \(x\) приращение \(\Delta y\to0\) , если только \(\Delta x\to0\) поэтому функция непрерывна при всех действительных значениях переменной \(x\) .
Пример 2. Доказать непрерывность функции \(y=\frac{1}{x-1}\) в точке \(x=3\) .
Решение. Для доказательства найдем приращение функции \(y\) при переходе значения аргумента от \(x=3\) к \(x=3+\Delta x\)
\(\Delta y=\frac{1}{3+\Delta x-1}-\frac{1}{3-1}=\frac{1}{2+\Delta x}-\frac{1}{2}=\frac{2-2-\Delta x}{2(2+\Delta x)}=\frac{-\Delta x}{2(2+\Delta x)}.\)
Найдем предел приращения функции при \(\Delta x\to0\)
\(\lim_{\Delta x\to0}\Delta y=-\lim_{\Delta x\to0}\frac{\Delta x}{2(2+\Delta x)}=-\frac{0}{2(2+0)}=0.\)
Так как предел приращения функции при \(\Delta x\to0\) равен нулю, то функция при \(x\to3\) непрерывна.
Пример 3. Определить характер разрыва функций и построить графики:
\(\mathrm{a)}~y=\frac{1}{x-1}~\text{if}~x=1;\qquad\mathrm{b)}~y=\frac{x}{|x|}~\text{if}~x=0;\qquad\mathrm{c)}~y=\begin{cases}2x,&\text{if}~x\ne2,\\1,&\text{if}~x=2;\end{cases}\qquad\mathrm{d)}~y=a^{1/x}~(a>1);\qquad\mathrm{e)}~y=\operatorname{arctg}\frac{1}{x}.\)
Решение.
a) При \(x=1\) функция не определена, найдём односторонние пределы в этой точки:
\(\lim_{x\to1-0}\frac{1}{x-1}=-\infty;\quad\lim_{x\to1+0}\frac{1}{x-1}=+\infty.\)
Следовательно, в точке \(x=1\) функция имеет разрыв второго рода.
b) При \(x<0\) предел функции равен \(\lim_{0-0}\frac{x}{|x|}=-1=k_1\) . При \(x>0\) предел равен \(\lim_{0+0}\frac{x}{|x|}=1=k_2\) . Следовательно, в точке \(x=1\) функция \(y\) имеет разрыв первого рода и скачок функции равен \(|k_1-k_2|=|-1-1|=2\) .
c) Функция определена на всей числовой оси, неэлементарная, так как в точке \(x=2\) аналитическое выражение функции меняется. Исследуем непрерывность функции в точке \(x=2\) :
\(\lim_{x\to2-0}=4,\quad\lim_{x\to2+0}2x=4,\quad y(2)=1,\quad k_1=k_2\ne k_3.\)
Очевидно, что в точке \(x=2\) функция имеет устранимый разрыв.
d) Найдём левый и правый пределы функции в точке \(x=0\) :
\(y(+0)=\lim_{x\to+0}a^{1/x}=+\infty,\quad y(-0)=\lim_{x\to-0}a^{1/x}=0.\)
Итак, в точке \(x=0\) справа функция имеет разрыв второго рода, а слева – непрерывность.
e) Найдём односторонние пределы функции в точке \(x=0\) :
\(y(+0)=\lim_{x\to+0}\operatorname{arctg}\frac{1}{x}=\frac{\pi}{2},\quad y(-0)=\lim_{x\to-0}\operatorname{arctg}\frac{1}{x}=-\frac{\pi}{2}.\)
Итак, в точке \(x=0\) с обеих сторон у функции \(y=\operatorname{arctg}\frac{1}{x}\) скачки.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Определение. Пусть функция у = f(x) определена в точке x0 и некоторой её окрестности. Функция у = f(x) называется непрерывной в точке x0 , если:
1. существует
2. этот предел равен значению функции в точке x0: ![]()
При определении предела подчёркивалось, что f(x) может быть не определена в точке x0, а если она определена в этой точке, то значение f(x0) никак не участвует в определении предела. При определении непрерывности принципиально, что f(x0) существует, и это значение должно быть равно lim f(x).
Определение.
Пусть функция у = f(х) определена в точке x0 и некоторой её окрестности. Функция f(x) называется непрерывной в точке x0, если для всех ε>0 существует положительное число δ, такое что для всех x из δ-окрестности точки x0 (т.е. |х-x0|
Здесь учитывается, что значение предела должно быть равно f(x0), поэтому, по сравнению с определением предела, снято условие проколотости δ-окрестности 0
Дадим ещё одно (равносильное предыдущим) определение в терминах приращений. Обозначим Δх = x - x0, эту величину будем называть приращением аргумента. Так как х->x0, то Δх->0, т е. Δх - б.м. (бесконечно малая) величина. Обозначим Δу = f(х)-f(x0), эту величину будем называть приращением функции, так как |Δу| должно быть (при достаточно малых |Δх|) меньше произвольного числа ε>0, то Δу- тоже б.м. величина, поэтому
Определение. Пусть функция у = f(х) определена в точке x0 и некоторой её окрестности. Функция f(х) называется непрерывной в точке x0 , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Определение. Функция f(х), не являющаяся непрерывной в точке x0, называется разрывной в этой точке.
Определение. Функция f(х) называется непрерывной на множестве X, если она непрерывна в каждой точке этого множества.
Теорема о непрерывности суммы, произведения, частного

Теорема о переходе к пределу под знаком непрерывной функции

Теорема о непрерывности суперпозиции непрерывных функций

Пусть функция f(x) определена на отрезке и монотонна на этом отрезке. Тогда f(x) может иметь на этом отрезке только точки разрыва первого рода.
Теорема о промежуточном значении. Если функция f(x) непрерывна на отрезке и в двух точках а и b (a меньше b) принимает неравные значения A = f(a) ≠ В = f(b), то для любого числа С, лежащего между А и В, найдётся точка c ∈ , в которой значение функции равно С: f(c) = C.
Теорема об ограниченности непрерывной функции на отрезке. Если функция f(x) непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема о достижении минимального и максимального значений. Если функция f(x) непрерывна на отрезке, то она достигает на этом отрезке свои нижнюю и верхнюю грани.
Теорема о непрерывности обратной функции. Пусть функция y=f(x) непрерывна и строго возрастает (убывает) на отрезке [а,b]. Тогда на отрезке существует обратная функция х = g(y), также монотонно возрастающая (убывающая) на и непрерывная.