Тема №11
На практике для задания случайных величин общего вида обычно используется функция распределения.
Вероятность того, что случайная величина х примет определенное значение х 0 , выражается через функцию распределения по формуле
р (х = х 0) = F(x 0 +0) – F(x 0). (3)
В частности, если в точке х = х 0 функция F(x) непрерывна, то
р (х = х 0) =0.
Случайная величина х с распределением р(А) называется дискретной, если на числовой прямой существует конечное или счетное множество W, такое, что р (W,) = 1.
Пусть W = {x 1 , x 2 ,…} и p i = p ({x i }) = p (x = x i ), i = 1,2,….Тогда для любого борелевского множества А вероятность р(А) определяется однозначно формулой
Положив в этой формуле А = {x i / x i < x}, x Î R , получим формулу для функции распределения F(x) дискретной случайной величины х :
F(x) = p (x < x ) =. (5)
График функции F(x)
представляет собой ступенчатую линию. Скачки функции F(x)
в точках х = х 1 , х 2 …(x 1
Пример 1. Найдите функцию распределения
дискретной случайной величины х из примера 1§ 13.
Используя функцию распределения, вычислите
вероятности событий: х < 3, 1 £ x < 4, 1 £ x £ 3.

|
|
полученной в § 13, и формулу (5), получим
функцию распределения:

По формуле (1) Р(x < 3) = F(3) = 0,1808; по формуле (2)
р(1 £ x < 4) = F (4) – F(1) = 0,5904 – 0,0016 = 0,5888;
p (1 £ x £ 3) = p (1 £ x <3) + p(x = 3) = F(3) – F(1) + F(3+0) – F(3) =
F(3+0) – F(1) = 0,5904 – 0,0016 = 0,5888.
Пример 2. Дана функция

Является ли функция F(x) функцией распределения некоторой случайной величины? В случае положительного ответа найдите ![]() . Построить график функции F(x).
. Построить график функции F(x).
Решение. Для того чтобы наперед заданная функция F(x) являлась функцией распределения некоторой случайной величины х, необходимо и достаточно выполнение следующих условий (характеристических свойств функции распределения):
1.  F(x) – неубывающая функция.
F(x) – неубывающая функция.
3. При любом х Î R F(x – 0) = F(x ).
Для заданной функции F(x) выполнение
этих условий очевидно. Значит,
F(x) – функция распределения.
Вероятность  вычисляем по
вычисляем по
формуле (2):
График функции F(x ) представлен на рисунке 13.
Пример 3. Пусть F 1 (x ) и F 2 (x ) – функции распределения случайных величин х 1 и х 2 соответственно, а 1 и а 2 – неотрицательные числа, сумма которых равна 1.
Доказать, что F(x ) = a 1 F 1 (x ) + a 2 F 2 (x ) является функцией распределения некоторой случайной величины х .
Решение. 1) Так как F 1 (x ) и F 2 (x ) – неубывающие функции и а 1 ³ 0, а 2 ³ 0, то a 1 F 1 (x ) и a 2 F 2 (x ) - неубывающие, следовательно, их сумма F(x ) тоже неубывающая.
3) При любом х Î R F(x - 0) = a 1 F 1 (x - 0) + a 2 F 2 (x - 0)= a 1 F 1 (x ) + a 2 F 2 (x ) = F(x ).
Пример 4. Дана функция

Является ли F(x) функцией распределения случайной величины?
Решение. Легко заметить, что F(1) = 0,2 > 0,11 = F(1,1). Следовательно, F(x ) не является неубывающей, а значит, не является функцией распределения случайной величины. Заметим, что остальные два свойства для данной функции справедливы.
Контрольное задание №11
1. Дискретная случайная величина х
x ) и, используя ее, найдите вероятности событий: а) –2 £ х < 1; б) ½х ½£ 2. Постройте график функции распределения.
3. Дискретная случайная величина х задана таблицей распределения:
| x i | |||||
| p i | 0,05 | 0,2 | 0,3 | 0,35 | 0,1 |
Найдите функцию распределения F(x ) и найдите вероятности следующих событий: а) x < 2; б) 1 £ х < 4; в) 1 £ х £ 4; г) 1 < x £ 4; д) х = 2,5.
4. Найдите функцию распределения дискретной случайной величины х , равной числу выпавших очков при одном бросании игральной кости. Используя функцию распределения, найдите вероятность того, что выпадет не менее 5 очков.
5. Производятся последовательные испытания 5 приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Составьте таблицу распределения и найдите функцию распределения случайного числа испытаний приборов, если вероятность выдержать испытания для каждого прибора 0,9.
6. Задана функция распределения дискретной случайной величины х :

а) Найдите вероятность события 1 £ х £ 3.
б) Найдите таблицу распределения случайной величины х .
7. Задана функция распределения дискретной случайной величины х :

Составьте таблицу распределения данной случайной величины.
8. Монету бросают n раз. Составьте таблицу распределения и найдите функцию распределения числа появлений герба. Постройте график функции распределения при n = 5.
9. Монету бросают, пока не выпадет герб. Составьте таблицу распределения и найдите функцию распределения числа появлений цифры.
10. Снайпер стреляет по цели до первого попадания. Вероятность промаха при отдельном выстреле равна р . Найдите функцию распределения числа промахов.
Функция распределения вероятностей случайной величины и ее свойства.
Рассмотрим функцию F(х) , определенную на всей числовой оси следующим образом: для каждого х значение F(х) равно вероятности того, что дискретная случайная величина примет значение, меньшее х , т. е.
| | (18) |
Эта функция называется функцией распределения вероятностей , или кратко, функцией распределения .
Пример 1. Найти функцию распределения случайной величины , приведенной в примере 1, п. 1.
Решение: Ясно, что если , то F(x)=0 , так как не принимает значений, меньших единицы. Если , то ; если , то . Но событие <3 в данном случае является суммой двух несовместных событий: =1 и =2. Следовательно,
Итак для имеем F(x)=1/3
. Аналогично вычисляются значения функции в промежудках , и . Наконец, если x>6
то F(x)=1
, так как в этом случае любое возможное значение (1, 2, 3, 4, 5, 6)
меньше, чем x
. График функции F(x)
изображен на рис. 4.

Пример 2. Найти функцию распределения случайной величины , приведенной в примере 2, п. 1.
Решение: Очевидно, что


График F(x)
изображен на рис. 5.

Зная функцию распределения F(x)
, легко найти вероятность того, что случайная величина удовлетворяет неравенствам .
Рассмотрим событие, заключающееся в том, что случайняя величина примет значение, меньшее . Это событие распадается на сумму двух несовместных событий: 1) случайная величина принимает значения, меньшие , т.е. ; 2) случайная величина принимает значения, удовлетворяющие неравенствам . Используя аксиому сложения, получаем
Но по определению функции распределения F(x)
[см. формулу (18)], имеем ![]() ,
, ![]() ; cледовательно,
; cледовательно,
| (19) |
Таким образом, вероятность попадания дискретной случайной величины в интервал равна приращению функции распределения на этом интервале.
Рассмотрим основные свойства функции распределения.
1°. Функция распределения является неубывающей.
В самом деле, пусть < . Так как вероятность любого события неотрицательна, то ![]() . Поэтому из формулы (19) следует, что
. Поэтому из формулы (19) следует, что ![]() , т.е.
, т.е. ![]() .
.
2°. Значения функции распределения удовлетворяют неравенствам
.
Это свойство вытекает из того, что F(x)
определяется как вероятность [см. формулу (18)]. Ясно, что * и .
3°. Вероятность того, что дискретная случайная величина примет одно из возможных значений xi, равна скачку функции распределения в точке xi
.
Действительно, пусть xi
- значение, принимаемое дискретной случайной величиной, и . Полагая в формуле (19) , , получим
Т.е. значение p(xi)
равно скачку функции ** xi
. Это свойство наглядно иллюстрируется на рис. 4 и рис. 5.
* Здесь и в дальнейшем введены обозначения: ![]() ,
, ![]() .
.
** Можно показать, что F(xi)=F(xi-0)
, т.е. что функция F(x)
непрерывна слева в точке xi
.
3. Непрерывные случайные величины.
Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х)
. Однако их можно задать с помощью функции распределения вероятностей F(х)
. Эта функция определяется точно так же, как и в случае дискретной случайной величины:
![]()
Таким образом, и здесь функция F(х)
определена на всей числовой оси, и ее значение в точке х
равно вероятности того, что случайная величина примет значение, меньшее чем х
.
Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.
Случайная величина называется непрерывной
, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x
равенству
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием , ограниченной сверху кривой (рис. 6).

Так как , а на основании формулы (22)

Заметим, что для непрерывной случайной величины функция распределения F(х)
непрерывна в любой точке х
, где функция непрерывна. Это следует из того, что F(х)
в этих точках дифференцируема.
На основании формулы (23), полагая x 1 =x
, , имеем
В силу непрерывности функции F(х)
получим, что
![]()
Следовательно
Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю
.
Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств
Имеют одинаковую вероятность, т.е.
В самом деле, например,
Так как
Замечание.
Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x 1
как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x 1
. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.
Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.
Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной , если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала. Для непрерывной случайной величины невозможно указать все возможные значения, поэтому обозначают интервалы этих значений, которые связаны с определёнными вероятностями.
Примерами непрерывных случайных величин могут служить: диаметр детали, обтачиваемой до заданного размера, рост человека, дальность полёта снаряда и др.
Так как для непрерывных случайных величин функция F (x ), в отличие от дискретных случайных величин , нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю.
Это значит, что для непрерывной случайной величины бессмысленно говорить о распределении вероятностей между её значениями: каждое из них имеет нулевую вероятность. Однако в некотором смысле среди значений непрерывной случайной величины есть "более и менее вероятные". Например, вряд ли у кого-либо возникнет сомнение, что значение случайной величины - роста наугад встреченного человека - 170 см - более вероятно, чем 220 см, хотя и одно, и другое значение могут встретиться на практике.
Функция распределения непрерывной случайной величины и плотность вероятности
В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, вводится понятие плотности распределения или плотности вероятности. Подойдём к нему путём сравнения смысла функции распределения для непрерывной случайной величины и для дискретной случайной величины.
Итак, функцией распределения случайной величины (как дискретной, так и непрерывной) или интегральной функцией называется функция , которая определяет вероятность, что значение случайной величины X меньше или равно граничному значению х .
Для дискретной случайной величины в точках её значений x 1 , x 2 , ..., x i ,... сосредоточены массы вероятностей p 1 , p 2 , ..., p i ,... , причём сумма всех масс равна 1. Перенесём эту интерпретацию на случай непрерывной случайной величины. Представим себе, что масса, равная 1, не сосредоточена в отдельных точках, а непрерывно "размазана" по оси абсцисс Оx с какой-то неравномерной плотностью. Вероятность попадания случайной величины на любой участок Δx будет интерпретироваться как масса, приходящаяся на этот участок, а средняя плотность на этом участке - как отношение массы к длине. Только что мы ввели важное понятие теории вероятностей: плотность распределения.
Плотностью вероятности f (x ) непрерывной случайной величины называется производная её функции распределения:
![]() .
.
Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a ; b ]:

вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a ; b ], равна определённому интегралу от её плотности вероятности в пределах от a до b :
![]()
![]() .
.
При этом общая формула функции F (x ) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f (x ) :
![]() .
.
График плотности вероятности непрерывной случайной величины называется её кривой распределения (рис. ниже).

Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох , графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b .
Свойства функции плотности вероятности непрерывной случайной величины
1. Вероятность того, что случайная величина примет какое-либо значение из интервала (и площадь фигуры, которую ограничивают график функции f (x ) и ось Ох ) равна единице:
2. Функция плотности вероятности не может принимать отрицательные значения:
а за пределами существования распределения её значение равно нулю
Плотность распределения f (x ), как и функция распределения F (x ), является одной из форм закона распределения, но в отличие от функции распределения, она не универсальна: плотность распределения существует только для непрерывных случайных величин.
Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.
Если функция плотности распределения f (x ) непрерывной случайной величины в некотором конечном интервале [a ; b ] принимает постоянное значение C , а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным .
Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным .
Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:
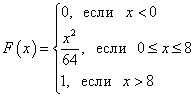
Найти функцию f (x ) плотности вероятности непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8: .
Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:

График функции F (x ) - парабола:

График функции f (x ) - прямая:

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:
Пример 2. Функция плотности вероятности непрерывной случайной величины дана в виде:
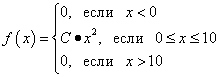
Вычислить коэффициент C . Найти функцию F (x ) распределения вероятностей непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что непрерывная случайная величина примет какое-либо значение в интервале от 0 до 5: .
Решение. Коэффициент C найдём, пользуясь свойством 1 функции плотности вероятности:

Таким образом, функция плотности вероятности непрерывной случайной величины:

Интегрируя, найдём функцию F (x ) распределения вероятностей. Если x < 0 , то F (x ) = 0 . Если 0 < x < 10 , то
![]() .
.
x > 10 , то F (x ) = 1 .
Таким образом, полная запись функции распределения вероятностей:

График функции f (x ) :

График функции F (x ) :

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 0 до 5:
Пример 3. Плотность вероятности непрерывной случайной величины X задана равенством , при этом . Найти коэффициент А , вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[, функцию распределения непрерывной случайной величины X .
Решение. По условию приходим к равенству

Следовательно, , откуда . Итак,
![]() .
.
Теперь находим вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[:

Теперь получим функцию распределения данной случайной величины:
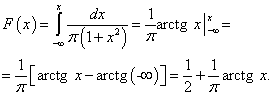
Пример 4.
Найти плотность вероятности непрерывной
случайной величины X
, которая принимает только неотрицательные значения, а
её функция распределения ![]() .
.
Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей и плотности для функции двух случайных аргументов.
Закон распределения вероятностей функции одной случайной величины
При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.
Таким образом, возникает задача, которую можно сформулировать так.
Дана система случайных величин (X_1,X_2,\ldots,X_n) , закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:
Y=\varphi(X_1,X_2,\ldots,X_n).
Требуется определить закон распределения случайной величины Y , зная вид функций (6.1) и закон совместного распределения ее аргументов.
Рассмотрим задачу о законе распределения функции одного случайного аргумента
Y=\varphi(X).
\begin{array}{|c|c|c|c|c|}\hline{X}&x_1&x_2&\cdots&x_n\\\hline{P}&p_1&p_2&\cdots&p_n\\\hline\end{array}
Тогда Y=\varphi(X) также дискретная случайная величина с возможными значениями . Если все значения y_1,y_2,\ldots,y_n различны, то для каждого k=1,2,\ldots,n события \{X=x_k\} и \{Y=y_k=\varphi(x_k)\} тождественны. Следовательно,
P\{Y=y_k\}=P\{X=x_k\}=p_k
и искомый ряд распределения имеет вид
\begin{array}{|c|c|c|c|c|}\hline{Y}&y_1=\varphi(x_1)&y_2=\varphi(x_2)&\cdots&y_n=\varphi(x_n)\\\hline{P}&p_1&p_2&\cdots&p_n\\\hline\end{array}
Если же среди чисел y_1=\varphi(x_1),y_2=\varphi(x_2),\ldots,y_n=\varphi(x_n) есть одинаковые, то каждой группе одинаковых значений y_k=\varphi(x_k) нужно отвести в таблице один столбец и соответствующие вероятности сложить.
Для непрерывных случайных величин задача ставится так: зная плотность распределения f(x) случайной величины X , найти плотность распределения g(y) случайной величины Y=\varphi(X) . При решении поставленной задачи рассмотрим два случая.
Предположим сначала, что функция y=\varphi(x) является монотонно возрастающей, непрерывной и дифференцируемой на интервале (a;b) , на котором лежат все возможные значения величины X . Тогда обратная функция x=\psi(y) существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем
G(y)=f\bigl(\psi(y)\bigr)\cdot |\psi"(y)|.
Пример 1. Случайная величина X распределена с плотностью
F(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2}
Найти закон распределения случайной величины Y , связанной с величиной X зависимостью Y=X^3 .
Решение. Так как функция y=x^3 монотонна на промежутке (-\infty;+\infty) , то можно применить формулу (6.2). Обратная функция по отношению к функции \varphi(x)=x^3 есть \psi(y)=\sqrt{y} , ее производная \psi"(y)=\frac{1}{3\sqrt{y^2}} . Следовательно,
G(y)=\frac{1}{3\sqrt{2\pi}}e^{-\sqrt{y^2}/2}\frac{1}{\sqrt{y^2}}
Рассмотрим случай немонотонной функции. Пусть функция y=\varphi(x) такова, что обратная функция x=\psi(y) неоднозначна, т. е. одному значению величины y соответствует несколько значений аргумента x , которые обозначим x_1=\psi_1(y),x_2=\psi_2(y),\ldots,x_n=\psi_n(y) , где n - число участков, на которых функция y=\varphi(x) изменяется монотонно. Тогда
G(y)=\sum\limits_{k=1}^{n}f\bigl(\psi_k(y)\bigr)\cdot |\psi"_k(y)|.
Пример 2. В условиях примера 1 найти распределение случайной величины Y=X^2 .
Решение. Обратная функция x=\psi(y) неоднозначна. Одному значению аргумента y соответствуют два значения функции x
Применяя формулу (6.3), получаем:
\begin{gathered}g(y)=f(\psi_1(y))|\psi"_1(y)|+f(\psi_2(y))|\psi"_2(y)|=\\\\=\frac{1}{\sqrt{2\pi}}\,e^{-\left(-\sqrt{y^2}\right)^2/2}\!\left|-\frac{1}{2\sqrt{y}}\right|+\frac{1}{\sqrt{2\pi}}\,e^{-\left(\sqrt{y^2}\right)^2/2}\!\left|\frac{1}{2\sqrt{y}}\right|=\frac{1}{\sqrt{2\pi{y}}}\,e^{-y/2}.\end{gathered}
Закон распределения функции двух случайных величин
Пусть случайная величина Y является функцией двух случайных величин, образующих систему (X_1;X_2) , т. е. Y=\varphi(X_1;X_2) . Задача состоит в том, чтобы по известному распределению системы (X_1;X_2) найти распределение случайной величины Y .
Пусть f(x_1;x_2) - плотность распределения системы случайных величин (X_1;X_2) . Введем в рассмотрение новую величину Y_1 , равную X_1 , и рассмотрим систему уравнений
Будем полагать, что эта система однозначно разрешима относительно x_1,x_2
и удовлетворяет условиям дифференцируемости.
Плотность распределения случайной величины Y
G_1(y)=\int\limits_{-\infty}^{+\infty}f(x_1;\psi(y;x_1))\!\left|\frac{\partial\psi(y;x_1)}{\partial{y}}\right|dx_1.
Заметим, что рассуждения не изменяются, если введенную новую величину Y_1 положить равной X_2 .
Математическое ожидание функции случайных величин
На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.
Пусть случайная величина Y является функцией случайного аргумента X с заданным законом распределения
Y=\varphi(X).
Требуется, не находя закона распределения величины Y , определить ее математическое ожидание
M(Y)=M[\varphi(X)].
Пусть X - дискретная случайная величина, имеющая ряд распределения
\begin{array}{|c|c|c|c|c|}\hline{x_i}&x_1&x_2&\cdots&x_n\\\hline{p_i}&p_1&p_2&\cdots&p_n\\\hline\end{array}
Составим таблицу значений величины Y и вероятностей этих значений:
\begin{array}{|c|c|c|c|c|}\hline{y_i=\varphi(x_i)}&y_1=\varphi(x_1)&y_2=\varphi(x_2)&\cdots&y_n=\varphi(x_n)\\\hline{p_i}&p_1&p_2&\cdots&p_n\\\hline\end{array}
Эта таблица не является рядом распределения случайной величины Y , так как в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины Y можно определить по формуле
M[\varphi(X)]=\sum\limits_{i=1}^{n}\varphi(x_i)p_i,
так как величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен.
Формула (6.4) не содержит в явном виде закон распределения самой функции \varphi(X) , а содержит только закон распределения аргумента X . Таким образом, для определения математического ожидания функции Y=\varphi(X) вовсе не требуется знать закон распределения функции \varphi(X) , а достаточно знать закон распределения аргумента X .
Для непрерывной случайной величины математическое ожидание вычисляется по формуле
M[\varphi(X)]=\int\limits_{-\infty}^{+\infty}\varphi(x)f(x)\,dx,
где f(x) - плотность распределения вероятностей случайной величины X .
Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знание даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сформулируем эти случаи в виде теорем.
Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:
M(X+Y)=M(X)+M(Y).
Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
M(XY)=M(X)M(Y)+\mu_{xy}.
Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.
Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Дисперсия функции случайных величин
По определению дисперсии имеем D[Y]=M[(Y-M(Y))^2]. . Следовательно,
D[\varphi(x)]=M[(\varphi(x)-M(\varphi(x)))^2] , где .
Приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента Y=\varphi(X) дисперсия выражается формулой
D[\varphi(x)]=\int\limits_{-\infty}^{+\infty}(\varphi(x)-M(\varphi(x)))^2f(x)\,dx,
где M(\varphi(x))=M[\varphi(X)] - математическое ожидание функции \varphi(X) ; f(x) - плотность распределения величины X .
Формулу (6.5) можно заменить на следующую:
D[\varphi(x)]=\int\limits_{-\infty}^{+\infty}\varphi^2(x)f(x)\,dx-M^2(X)
Рассмотрим теоремы о дисперсиях , которые играют важную роль в теории вероятностей и ее приложениях.
Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:
D\!\left[\sum\limits_{i=1}^{n}X_i\right]=\sum\limits_{i=1}^{n}D+2\sum\limits_{i Следствие 6.3.
Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых: D\!\left[\sum\limits_{i=1}^{n}X_i\right]=\sum\limits_{i=1}^{n}D
\mu_{y_1y_2}= M(Y_1Y_2)-M(Y_1)M(Y_2).
\mu_{y_1y_2}=M(\varphi_1(X)\varphi_2(X))-M(\varphi_1(X))M(\varphi_2(X)).
Рассмотрим основные свойства корреляционного момента и коэффициента корреляции
. Свойство 1.
От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не изменяются. Свойство 2.
Для любых случайных величин X
и Y
абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин: |\mu_{xy}|\leqslant\sqrt{D[X]\cdot D[Y]}=\sigma_x\cdot \sigma_y,
Функцией распределения случайной величины X называется функция F(x), выражающая для каждого х вероятность того, что случайная величина X примет значение
, меньшее х
Пример 2.5. Дан ряд распределения случайной величины Найти и изобразить графически ее функцию распределения. Решение. В соответствии с определением F(jc) = 0 при х
х
F(x) =
0,4 + 0,1 = 0,5 при 4 F{x) = 0,5 + 0,5 = 1 при х
> 5. Итак (см. рис. 2.1): Свойства функции распределения: 1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. при х
2
>х
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности - равна единице, т.е. 4. Вероятность попадания случайной величины X
в интервал
равна определенному интегралу от ее плотности вероятности в пределах от а
до b
(см. рис. 2.2), т.е.
Рис. 2.2 3. Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле: F(x)=
Jp (*)*. (2.10) 4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: Геометрически свойства / и 4
плотности вероятности означают, что ее график - кривая распределения
- лежит не ниже оси абсцисс
, и полная площадь фигуры
, ограниченной кривой распределения и осью абсцисс
, равна единице.
Для непрерывной случайной величины X
математическое ожидание М(Х)
и дисперсия D(X)
определяются по формулам: (если интеграл абсолютно сходится); или
(если приведенные интегралы сходятся). Наряду с отмеченными выше числовыми характеристиками для описания случайной величины используется понятие квантилей и процентных точек. Квантилем уровня q
(или q-квантилем) называется такое значение
x q
случайной величины
, при котором функция ее распределения принимает значение
, равное q,
т. е. По данным примера 2.6 найти квантиль xqj и 30%-ную точку случайной величины X.
Решение. По определению (2.16) F(xo t3)= 0,3, т. е. ~Y~ =
0,3, откуда квантиль х 0
3 = 0,6. 30%-ная точка случайной величины X
, или квантиль Х)_о,з = xoj
» находится аналогично из уравнения ^ = 0,7 . откуда *,= 1,4. ? Среди числовых характеристик случайной величины выделяют начальные
v* и центральные
р* моменты к-го порядка
, определяемые для дискретных и непрерывных случайных величин по формулам:
т. е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.

![]()
![]()


